N Queens

각 알고리즘의 이해) BF/ DFS/ Backtraking
자료구조의 이해) recursion, tree (+graph)
문제 유형 살펴보기) N-Queens problems
문제 이해) N-Queens
정석된 풀이, 다양한 풀이

🔥 1. BF/ DFS/ Backtraking

1. Brute(무식한) + Force(힘)

브루트 포스는 완전 탐색 알고리즘으로 가능한 모든 경우의 수를 탐색하고 조건에 맞는 결과만 가져오는 알고리즘. 무식하게 모두 탐색하여 결과를 찾는 방식이기 때문에 100% 정답을 찾는다.

'해가 하나 이상 존재한다'라는 가정을 세우고 모든 영역을 탐색
모든 자료를 탐색해야 하므로 구조마다 방법이 다름.
선형 구조를 모두 탐색하는 방법: 순차탐색
비선형 구조를 모두 탐색하는 방법: BFS(너비 우선 탐색/ 큐(Queue) 사용),DFS(깊이 우선 탐색/ 스택(Stack) 사용)

2. DFS(깊이 우선 탐색)

연결되어 있는 노드들의 우선순위에 따라 최대한 깊게 들어가는 방법
따라서, 불필요할 것 같은 경로를 사전에 차단하거나 하는 등의 행동이 없으므로 경우의 수를 줄이지 못한다.
탐색 시 어떤 노드를 방문했었는지를 검사해야 한다. 이를 검사하지 않을 경우 무한 루프에 빠질 수 있다.
문제 풀이 방법: iterative(stack), recursion

3. Backtraking(백트레킹)

모든 가능한 경우의 수 중에서 특정한 조건을 만족하는 경우만 살펴보는 방법
즉, 답이 될 만한지 판단하고 그렇지 않으면 그 부분까지 탐색하는 것을 하지 않고 가지치기 하는 것
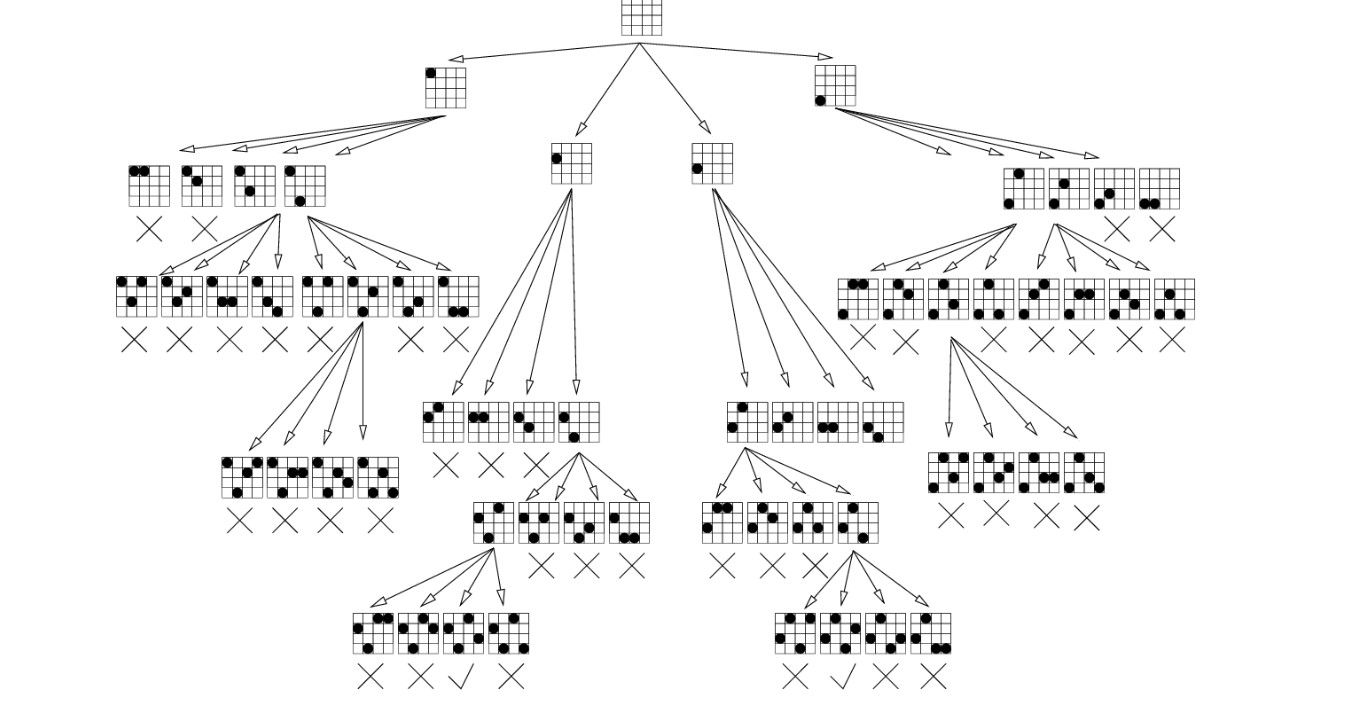
n=1, n=2, n=3 노드를 내려가면서 해가 될 만한지 판단한 후 유망하지 않다고 결정되면 그 노드의 이전(부모) 노드로 돌아간다 해서 backtraking
주로 문제 풀이에서는 DFS 등으로 모든 경우의 수를 탐색하는 과정에서, 조건문 등을 걸어 답이 절대로 될 수 없는 상황을 정의하고, 그러한 상황일 경우에는 탐색을 중지시킨 뒤 그 이전으로 돌아가서 다시 다른 경우를 탐색하게끔 구현
recursion을 사용한다는 점에서 DFS와 유사성이 있음
답이 될 가능성이 있으면 유망하다(promising)고 하며, 유망하지 않은 노드에 가지 않는 것을 가지치기(pruning)라고 한다.
가지치기를 얼마나 잘하느냐에 따라 효율성이 결정
N-Queens
1) 어떤 식으로 '유망성(답이 될 가능성)'을 따질 것인가
2) 유망하지 않을 경우 어떤 식으로 가지치기(답이 안될 가능성 탐색 ㄴ)를 할 것인가

🔥 2. 자료구조) recursion, Graph와 tree

1. recursion

void Recursive(void)
{
  printf("Recursive call! \n");
  Recursive();  # 나자신 호출
}

# 재귀함수: 다음과 같이 함수 내에서 자기 자신을 다시 호출하는 함수를 의미
# Q) 완료되지 않은 함수를 다시 호출하는 것이 가능한가요!? 
# A) 네! recursive 함수가 호출되면, recursive 함수의 복사본이 만들어져서 복사본이 실행되는 구조이기 때문입니다!

# 재귀의 탈출 조건이 정해져 있지 않으면 반환이 되지 않고 무한루프에 빠지게 된다
# 그러므로 재귀함수를 정의하는데 있어서 탈출조건을 구성하는 것은 매우 중요!

%%writefile test.cpp

# include <stdio.h>

void Recursive(int num)
{
    if(num <=0)
      return;
    printf("Recursive call! %d \n", num);
    Recursive(num-1);
}

int main(void)
{
    Recursive(3);
    return 0;
}

2. 그래프와 트리

	그래프	트리
정의	노드와 그 노드를 연결하는 간선으로 구성된 자료구조	그래프의 한 종류, 방향성이 있는 비순환 그래프
방향성	방향, 무방향 모두 존재	방향 그래프만 존재
사이클	순환, 비순환 모두 존재, 노드 한개의 자체 순환도 가능	비순환 그래프만 존재
루트노드	루트 노드의 개념이 없음	한 개의 루트 노드만이 존재
부모-자식	부모-자식의 개념이 없음	루트 노트를 제외한 노드는 1개의 부모노드만을 가짐
모델	네트워크 모델	계층 모델
순회	DFS, BFS	DFS, BFS 방식의 전위, 중위, 후위 순회
간선의 수	간선의 개수는 자유, 없을 수도 있음	N개의 노드를 가진 트리는 항상 N-1개의 간선을 가짐
예시 및 종류	지도, 최단경로, 선수과목	이진트리, 이진 탐색 트리, 이진 힙, 균형 트리

2-1. 트리(Tree)

정의: 트리는 계층적 관계를 표현하는 자료구조.
보통 자료구조하면 무엇인가 저장하고 꺼내오는 것이 전부인 것으로 이해할 수도 있다. 스택과 큐 처럼 선형 자료구조는 이에 초점이 맞춰져있기 때문. 하지만 자료구조는 근본적으로 무엇인가를 표현하는 도구이다. 표현을 위해서 저장과 삭제라는 기능이 제공되는 것임을 이해하는 것이 트리 이해의 첫 단계
즉 트리를 이용해서 무엇인가 저장하고 꺼내야 한다는 생각을 지우고 무엇인가 표현하는 도구라고 생각하는 게 트리 자료구조 이용의 key point!
트리는 위로 뻗느냐 아래로 뻗느냐가 중요한 게 아니라 가지를 늘려가며 뻗어간다는 사실이 중요.

2-3. 289. N-ary Tree Preorder Traversal

https://leetcode.com/problems/n-ary-tree-preorder-traversal/

def preorder(node):
    if node is None:
        return 
    print(node.val)
    preorder(node.left)
    preorder(node.right)

class Solution:
    def preorder(self, root: 'Node') -> List[int]:

        nodes = [] # 파이썬은 인접행렬을 리스트로 구현

        def pre(root): # preorder 순회니까 
            if not root: # root 에서 시작해야함! 
                return
            nodes.append(root.val) # root node append 
            for child in root.children: # root의 children을 차례로 반복문을 돌아서 돌고
                pre(child) # children 아래의 child들을 재귀함수로 불러서 다시 돌고
        pre(root) 
        return nodes # 담긴 노드의 리스트 반환

🔥 3. N-Queens problems

1) https://leetcode.com/problems/n-queens/
return all distinct solutions to the n-queens puzzle(Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively 즉 [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] 존재하는 answer 그대로 반환/ 1 <= n <= 9
2) https://leetcode.com/problems/n-queens-ii/
return the number of distinct solutions to the n-queens puzzle/ 1 <= n <= 9
3) https://programmers.co.kr/learn/courses/30/lessons/12952
return: n개의 퀸이 조건에 만족 하도록 배치할 수 있는 방법의 수/ n은 12이하의 자연수
4) https://www.acmicpc.net/problem/9663
return: 퀸 N개를 서로 공격할 수 없게 놓는 경우의 수를 출력/ (1 ≤ N < 15)

🔥 4. N-Queens 문제 이해, psudo code

N*N 체스판 존재
N 개의 Queen 존재. 각 퀸은 한 발자국 움직이면 서로를 공격할 수 있어서 treathen 즉 위협적인 존재임. 옆(row)으로, 위아래(col)으로, 대각선(dia)으로 이동 가능. 이런 queen이 N 개로 서로를 위협하지 않는 선에서 존재하려면 같은 행, 열, 대각선에 놓으면 안됨.
퀸을 놓는 게 불가능할 경우 더 이상 탐색하지 않고 바로 위의 노드로 돌아가서 탐색(pruning)

여기까지만 보면 for문 두번 돌려서 2차원 행렬을 구성해야 할 것 같지만! 잘 생각해 보면!!

체스판에 퀸을 놓을 때 어느 한 행에 퀸이 놓여있다면, 그 행에는 퀸을 절대 놓을 수 없기 떄문에 1차원 arr 가능!
퀸을 한 row에 놓고 같은 col과 dia는 놓을 수 없다.
promising: 같은 row checking
col, dia도 같은 방식으로 진행
다시 한번 check, 이렇게 노드를 체크하면서 유망한(promising) 한 노드만 남기고 유망하지 않은 노드는 가지치기(pruning) 하며 둘러보지 않는다는 점에서 DFS랑 차이점
만들 코드
Queen을 놓을 함수(i부터 끝까지)
promising 함수(col이 같거나, dia이 같거나 하면 false)

🔥 5. 정석

def solution(n):
    global answer
    answer = 0

    for i in range(n):
        col = [i] + [0]*(n-1) # col 정의 colㅣ[a] = 인 경우, b행 a열에 퀸이 위치해있다는 뜻
        check(0,col)
    return answer

def check(idx,col):
    global answer
    n=len(col)
    if promising(idx,col) :
        if idx==n-1: # 현재 열이 마지막 열일 경우 모든 열이 퀸들을 만족하므로 
            answer += 1
        else :
            for j in range(n):
                col[idx+1] = j # 다음 열에 대해 0부터 n-1행까지 경우에 대해 퀸 check!
                check(idx+1,col)

def promising(idx,col):
    for k in range(idx):
        if (col[idx]==col[k]) or (abs(col[idx]-col[k])==idx-k) :# 행이 같은 경우, 대각선에 있는 경우 pruning
            return False
    return True

def check(idx,col):
    global answer
    n=len(col)
    if promising(idx,col) :
        if idx==n-1:
            answer += 1
        else :
            for j in range(n):
                col[idx+1] = j
                check(idx+1,col)


def promising(idx,col):
    for k in range(idx):
        if (col[idx]==col[k]) or (abs(col[idx]-col[k])==idx-k) :
            return False
    return True

def solution(n):
    global answer
    answer = 0

    for i in range(n):
        col = [i] + [0]*(n-1)
        check(0,col)
    return answer

# 비슷한 다른 풀이


def possible(x, y, n, col): # promising 함수
    for i in range(x):
        # 같은 열에 위치하는지 or 같은 대각선에 위치하는지 확인
        if y == col[i] or abs(y - col[i]) == x - i:
            return False
    return True

def queen(x, n, col):

    # row가 끝까지 갔으면 성공!
    if x == n:
        return 1

    count = 0

    for y in range(n):
        # 다음 퀸을 놓을 수 있는 경우만 진행
        if possible(x, y, n, col):
            col[x] = y # x번째 row의 col index 저장 ex) col[0] = 2 0번째 행의 2번째 col에 놓여져 있다.
            count += queen(x+1, n, col) # row index 증가 후 호출

    return count

def solution(n):

    col = [0] * n

    # 0은 세로축의 시작점 
    # n은 맵의 크기
    # col은 row 의 index를 담기 위한 리스트
    answer = queen(0, n, col)

    return answer

0번째 행부터 n-1번째 행까지 순서대로 queen을 놓는다. 각 행에서는 0~n-1번째 열까지 queen을 놓는다. 이 때, 현재 queen이 놓인 자리가 valid하다면 다음 행에 대하여 dfs를 호출하고, 백트래킹 알고리즘들이 그렇듯 이후 queen_idx[i]를 리셋한다. 다만, 이 풀이방법에서는 1차원 array를 사용하므로 에서는 다음 for문이 돌면서 기존에 둔 queen의 위치를 지워버리기 때문에 굳이 리셋하지 않아도 된다. 이차원어레이를 사용했다면 반드시 리셋하는 과정이 필요하다.

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        queen_idx = [0 for _ in range(n)] # queen_idx[i] = x -> matrix[i][x]에 queen이 놓여있다
        answer = []

        # i-1번째 행까지 queen이 놓여있다는 가정 하에 i번째 행에 queen을 놓는다.
        def isValid(i: int) -> bool:
            for k in range(i):
                if queen_idx[k] == queen_idx[i] or abs(k-i) == abs(queen_idx[k]-queen_idx[i]): return False
            return True

        def dfs(i: int):
            if i == n:
                answer.append(list(map(lambda x: "".join(["Q" if x == idx else "." for idx in range(n)]), queen_idx)))
                return

            for j in range(n):
                queen_idx[i] = j
                if isValid(i):
                    dfs(i+1)

        dfs(0)
        return answer

참고)

https://www.geeksforgeeks.org/backtracking-introduction/
https://www.geeksforgeeks.org/n-queen-problem-backtracking-3/?ref=gcse

저작자표시